BCapplier Class Reference

Wrapper for user matrix-vector multiply that applies "essential" boundary conditions. More...

Collaboration diagram for BCapplier:

[legend]

Public Member Functions
	BCapplier (int cnt_, int base_, const int *dof_, const double *value_)
void	set_c (IFEM_Matrix_product_c A, void *ptr_)
void	set_f (IFEM_Matrix_product_f A, void *ptr_)
void	solve (ILSI_Solver s, ILSI_Param *p, int fem_mesh, int fem_entity, int length, int width, const double *b, double *x)
void	multiply (int length, int width, const double *u, double *Au)
Private Member Functions
void	userMultiply (int length, int width, const double *src, double *dest)
int	at (int bcIdx)
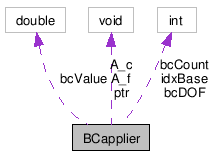
Private Attributes
IFEM_Matrix_product_c	A_c
IFEM_Matrix_product_f	A_f
void *	ptr
int	bcCount
	Definition of boundary conditions: for (i=0;i<bcCount;i++) assert(x[at(i)]==bcValue[i]).
int	idxBase
const int *	bcDOF
const double *	bcValue

---

Detailed Description

Wrapper for user matrix-vector multiply that applies "essential" boundary conditions.

The basic idea is that given a problem A x = b where x is only partially unknowns--that is, if x=u+c (Unknowns and boundary Conditions) A u + A c = b so there's an equivalent all-unknown system A u = b - A c = b' Now for A u = b', we have to just zero out all the boundary conditions.

Definition at line 137 of file ifem.C.

---

Constructor & Destructor Documentation

BCapplier::BCapplier	(	int	cnt_,
		int	base_,
		const int *	dof_,
		const double *	value_
	)			[inline]

Definition at line 161 of file ifem.C.

---

Member Function Documentation

void BCapplier::userMultiply	(	int	length,
		int	width,
		const double *	src,
		double *	dest
	)			[inline, private]

Definition at line 143 of file ifem.C.

References A_c, A_f, and ptr.

Referenced by multiply(), and solve().

Here is the caller graph for this function:

int BCapplier::at

(

int

bcIdx

)

[inline, private]

Definition at line 157 of file ifem.C.

References bcDOF, and idxBase.

Referenced by multiply(), and solve().

Here is the caller graph for this function:

void BCapplier::set_c	(	IFEM_Matrix_product_c	A,
		void *	ptr_
	)			[inline]

Definition at line 168 of file ifem.C.

References A_c, and ptr.

Referenced by IFEM_Solve_shared_bc().

Here is the caller graph for this function:

void BCapplier::set_f	(	IFEM_Matrix_product_f	A,
		void *	ptr_
	)			[inline]

Definition at line 171 of file ifem.C.

References A_f, and ptr.

Referenced by FTN_NAME().

Here is the caller graph for this function:

void BCapplier::solve	(	ILSI_Solver	s,
		ILSI_Param *	p,
		int	fem_mesh,
		int	fem_entity,
		int	length,
		int	width,
		const double *	b,
		double *	x
	)

Definition at line 202 of file ifem.C.

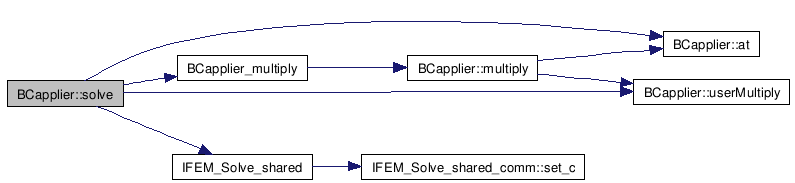
References at(), BCapplier_multiply(), bcCount, bcValue, c, IFEM_Solve_shared(), and userMultiply().

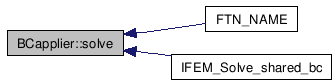
Referenced by FTN_NAME(), and IFEM_Solve_shared_bc().

Here is the call graph for this function:

Here is the caller graph for this function:

void BCapplier::multiply	(	int	length,
		int	width,
		const double *	u,
		double *	Au
	)			[inline]

Definition at line 181 of file ifem.C.

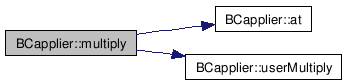
References at(), bcCount, and userMultiply().

Referenced by BCapplier_multiply().

Here is the call graph for this function:

Here is the caller graph for this function:

---

Field Documentation

IFEM_Matrix_product_c BCapplier::A_c [private]

Definition at line 139 of file ifem.C.

Referenced by set_c(), and userMultiply().

IFEM_Matrix_product_f BCapplier::A_f [private]

Definition at line 140 of file ifem.C.

Referenced by set_f(), and userMultiply().

void* BCapplier::ptr [private]

Definition at line 141 of file ifem.C.

Referenced by FTN_NAME(), set_c(), set_f(), and userMultiply().

int BCapplier::bcCount [private]

Definition of boundary conditions: for (i=0;i<bcCount;i++) assert(x[at(i)]==bcValue[i]).

Definition at line 154 of file ifem.C.

Referenced by FTN_NAME(), multiply(), and solve().

int BCapplier::idxBase [private]

Definition at line 155 of file ifem.C.

Referenced by at().

const int* BCapplier::bcDOF [private]

Definition at line 156 of file ifem.C.

Referenced by at(), and FTN_NAME().

const double* BCapplier::bcValue [private]

Definition at line 158 of file ifem.C.

Referenced by FTN_NAME(), and solve().

---

The documentation for this class was generated from the following file:

• libs/ck-libs/ifem/ifem.C